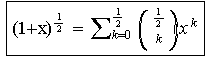und entsprechend
Lösung
Ein erster naiver Versuch einer Verallgemeinerung sieht wie folgt aus
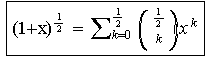und entsprechend
Das ist offensichtlich Unfug wegen der
oberen Grenzen in den Summen. Aber die Binomialkoeffitienten haben
ja die Eigenschaft
. Und damit läßt sich der Binomialsatz wie folgt schreiben
.
Man kann die obere Grenze (in der Summe) beliebig erhöhen, weil immer nur Nullen hinzukommen. Und diese Form des Binomialsatzes kann auf unsere neuen n-Werte verallgemeinert werden zu
Die Summanden der rechten Seite sind mit unserer Definition der Binomialkoeffizienten alle sinnvoll. Beispielsweise ist [-1]k=(-1)kk! wie man sofort nachrechnet! (Die übliche Definition bereitet dagegen Probleme, da n! nur für natürliches n erklärt ist.) Das gibt für die zweite Formel
,
was uns stark an die geometrische Reihe erinnert. Was bleibt, ist die Frage der Bedeutung der unendlich vielen Summanden. Um zu sehen, was dahinter stecken könnte, sollte man etwas numerisch experimentieren. Dabei findet man: Für kleine Werte von x wird die linke Seite unserer Gleichung durch endliche Summen der ersten Terme der rechten gut genähert. Und zwar immer besser, je mehr Summanden man mitnimmt. Für große Werte von x ergibt sich keine Konsistenz zwischen den beiden Seiten.
Ebenso ist es mit der ersten Formel für
n=1/2. Nehmen wir x=0.4. Dann setzen wir
.
N gibt also an, wieviele der ersten Summanden mitgenommen werden. Für
N=3 etwa 4. Dann finden wir folgende numerische Resultate
.
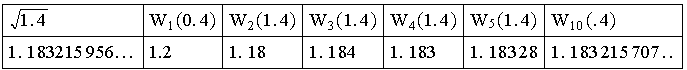Das legt die Vermutung nahe, dass die rechte Seite unserer erhaltenen neuartigen Gleichung eine Folge immer besserer Näherungen der linken liefert! Könnte das etwas wert sein? Sicher. Links wird die numerisch problematische Operation des Wurzelziehens verlangt. Für die rechte Seite dagegen werden immer nur einfache Rechenoperationen wie Multiplikation und Addition benötigt.