Inspektion
Die Aufgabe verlangt
einige Vorkenntnisse aus dem schulischen Bereich. Zunächst den
in Kap.1.3 des Vorkurses behandelten Binomialsatz. Sodann die
Schreibweise f(1)(x) für die erste Ableitung von
f(x). Für k=0 erhält man f(0)(x) und das steht
für die Funktion f(x) selbst.Ebenso f(2)(x) für
die zweite Ableitung. Für n=1 ergibt sich die „Produktregel
der Ableitung“. Dabei benutzen wir die in Kap.7 des Vorkurses
eingeführte Schreibweise für die Ableitung eines Produktes
an der Stelle x. Also (fg)´(x) anstelle (f(x)g(x))´ wie
vielfach üblich. In der Exponentialschreibweise (fg)(1)(x).
Wieder zerfällt die Aufgabe in mehrere Teilaufgaben. Dabei
ist die erste „erläutern und verstehen“ für uns
hier von besonderer Bedeutung. Man hat sich zu fragen: Was ist (zur
Konstruktion der beiden Rechenausdrücke) vorgegeben und was wird
damit gemacht? Zu jeder Seite der Gleichung gehört ein
bestimmter Rechenweg. Worum geht es? Um das zu verstehen, kann man
den dritten Aufgabenteil vorziehen und die Formel etwa für die
einfachen Fälle n=1,2 und 3 ausschreiben. Nun sieht man sofort,
dass die Formel allgemein eine Ableitungsregel angibt, die natürlich
zu beweisen ist. Bezeichnen würde man sie als „Produktregel
für die n-te Ableitung“. Die übliche Produktregel für
die erste Ableitung darf man (modular) als bekannt voraussetzen
Die drei Fälle:
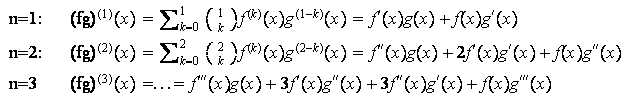 Für
n=1 ist das die übliche Produktregel. Gelten die beiden anderen
Gleichungen? Differenzieren der ersten als bereits bewiesen
vorausgestzten ergibt die zweite. Erneutes Differenzieren die dritte.
Das liefert bereits die Einstiegsidee für den geforderten
allgemeinen Beweis.
Für
n=1 ist das die übliche Produktregel. Gelten die beiden anderen
Gleichungen? Differenzieren der ersten als bereits bewiesen
vorausgestzten ergibt die zweite. Erneutes Differenzieren die dritte.
Das liefert bereits die Einstiegsidee für den geforderten
allgemeinen Beweis.
Nach einer derartigen Vorarbeit kann man sich an den
eigentlichen Beweis machen.
Zurück
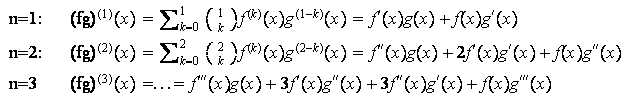 Für
n=1 ist das die übliche Produktregel. Gelten die beiden anderen
Gleichungen? Differenzieren der ersten als bereits bewiesen
vorausgestzten ergibt die zweite. Erneutes Differenzieren die dritte.
Das liefert bereits die Einstiegsidee für den geforderten
allgemeinen Beweis.
Für
n=1 ist das die übliche Produktregel. Gelten die beiden anderen
Gleichungen? Differenzieren der ersten als bereits bewiesen
vorausgestzten ergibt die zweite. Erneutes Differenzieren die dritte.
Das liefert bereits die Einstiegsidee für den geforderten
allgemeinen Beweis.